题目描述:
Given an m x n matrix of positive integers representing the height of each unit cell in a 2D elevation map, compute the volume of water it is able to trap after raining.
Note:
Both m and n are less than 110. The height of each unit cell is greater than 0 and is less than 20,000.
Example:
1 2 3 4 5 6 7 8 9 Given the following 3x6 height map: [ [1,4,3,1,3,2], [3,2,1,3,2,4], [2,3,3,2,3,1] ] Return 4.
[[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] before the rain.
这道题对于时间复杂度要求比较高, 轻易就会超时. 我的解法Runtime也不是很短, 有100多ms, 所以权当参考吧.
首先简单的对三维空间进行BFS是绝对超时, 因为最多有110*110*20000个坐标. 我一开始是使用分层进行BFS的办法, 确定每一层中不能装水的位置有多少. 之所以是搜索哪些不能装水而不是哪些能装水是因为搜索与边缘连通的位置只要从四条边开始搜索, 而搜索不与边缘连通的位置要从每个非边缘位置搜索, 数量要多得多.
有两种坐标是不能装水的:
与边缘连通的
该位置的高度比层数高的
拿总的面积减去不能装水的面积就是有水的面积, 把每一层的面积加起来就是最终的装水的体积. 但是这个办法是超时了, 我总结的超时原因是对每一层都从边缘开始BFS, 实际上并不需要每次都从最初始的情况开始BFS, 而可以在上一层的基础上进行BFS.
当层数为level的时候, 我们要检查的是height==level-1的坐标, 因为height>=level的坐标不能装水, 而height<level-1的坐标在之前的level已经计算过了, 那么对于所有的height==level-1的坐标有两种情况: 能存水和不能存水. 而区分条件是是否与边缘连通, 在知道上一层每个坐标与边缘连通情况(一个二维数组)的时候, 只要判断四周的坐标是否与边缘连通即可(因为已经不能存水的位置随着高度增加永远不能存水), 如果出现了一个height==level-1的坐标与边缘连通的情况, 那么就从这个点开始BFS, 能到达的坐标都是不能存水的.
在这种方法中, 二维平面上的每个点只有一次被BFS遍历到的机会, 大大降低了时间复杂度.
关于二维坐标表示: 二维坐标可以用pair来表示, 但是处理一个对象总没有用int来的快, 这道题由于长宽最大只有110, 所以完全可以把x,y坐标保存在一个int型中, 前16位保存x, 后16位保存y. int xy=x<<16|y, int x = xy>>16, y=xy&0xff.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 class Solution { int m, n, area; public : int trapRainWater (vector <vector <int >>& heightMap) int ans = 0 ; m = heightMap.size(); if (m == 0 ) return 0 ; n = heightMap[0 ].size(); area = n * m; priority_queue<int , vector <int >, greater<int >> pq; unordered_map <int , vector <int >> hm; for (int i = 0 ; i < m; i++){ for (int j = 0 ; j < n; j++){ pq.push(heightMap[i][j]); hm[heightMap[i][j]].push_back(xy2int(i, j)); } } vector <vector <int >> visited (m, vector <int >(n, 0 )) int edgeArea = 0 ; for (int i = 0 ; i < n; i++){ if (!visited[0 ][i]) edgeArea += BFS(heightMap, 0 , i, pq.top() + 1 , visited); if (!visited[m - 1 ][i]) edgeArea += BFS(heightMap, m - 1 , i, pq.top() + 1 , visited); } for (int i = 0 ; i < m; i++){ if (!visited[i][0 ]) edgeArea += BFS(heightMap, i, 0 , pq.top() + 1 , visited); if (!visited[i][n - 1 ]) edgeArea += BFS(heightMap, i, n - 1 , pq.top() + 1 , visited); } int t = pq.top(); while (!pq.empty() && pq.top() == t) pq.pop(); if (!pq.empty()){ int higherArea = pq.size(); ans += (area - higherArea - edgeArea) * (pq.top() - t); } while (!pq.empty()){ int level = pq.top() + 1 ; vector <int > &h = hm[level - 1 ]; for (auto i : h){ int x = i >> 16 , y = i & 0xff ; if (!visited[x][y] && (besideEdge(x, y, visited) || onEdge(x, y))){ edgeArea += BFS(heightMap, x, y, level, visited); } } while (!pq.empty() && pq.top() == level - 1 ) pq.pop(); if (pq.empty()) break ; int higherArea = pq.size(); ans += (area - higherArea - edgeArea) * (pq.top() - level + 1 ); } return ans; } int xy2int (int x, int y) return x << 16 | y; } bool besideEdge (int x, int y, vector <vector <int >> &visited) return ((x > 0 && visited[x - 1 ][y]) || (x < m - 1 && visited[x + 1 ][y]) || (y > 0 && visited[x][y - 1 ]) || (y < n - 1 && visited[x][y + 1 ])); } int BFS (vector <vector <int >>& heightMap, int i, int j, int k, vector <vector <int >> &visited) int ans = 0 ; if (heightMap[i][j] >= k) return 0 ; queue <int > q; q.push(xy2int(i, j)); visited[i][j] = 1 ; while (!q.empty()){ int curi = q.front() >> 16 , curj = q.front() & 0xff ; ans++; if (curi > 0 && !visited[curi - 1 ][curj] && heightMap[curi - 1 ][curj] < k){ q.push(xy2int(curi - 1 , curj)); visited[curi - 1 ][curj] = 1 ; } if (curi < m - 1 && !visited[curi + 1 ][curj] && heightMap[curi + 1 ][curj] < k){ q.push(xy2int(curi + 1 , curj)); visited[curi + 1 ][curj] = 1 ; } if (curj > 0 && !visited[curi][curj - 1 ] && heightMap[curi][curj - 1 ] < k){ q.push(xy2int(curi, curj - 1 )); visited[curi][curj - 1 ] = 1 ; } if (curj < n - 1 && !visited[curi][curj + 1 ] && heightMap[curi][curj + 1 ] < k){ q.push(xy2int(curi, curj + 1 )); visited[curi][curj + 1 ] = 1 ; } q.pop(); } return ans; } bool onEdge (int i, int j) return i == 0 || j == 0 || i == m - 1 || j == n - 1 ; } };
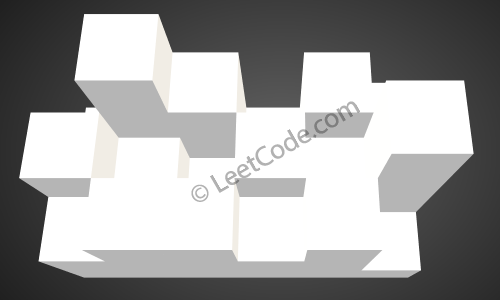 The above image represents the elevation map
The above image represents the elevation map 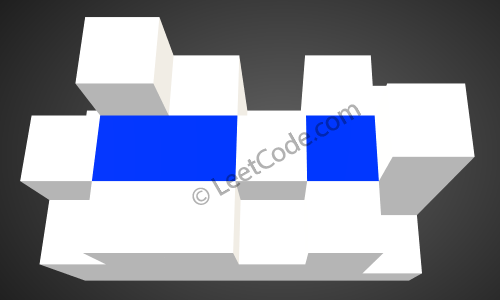 After the rain, water are trapped between the blocks. The total volume of water trapped is 4.
After the rain, water are trapped between the blocks. The total volume of water trapped is 4.