We write the integers of A and B (in the order they are given) on two separate horizontal lines.

Now, we may draw a straight line connecting two numbers A[i] and B[j] as long as A[i] == B[j], and the line we draw does not intersect any other connecting (non-horizontal) line.

Return the maximum number of connecting lines we can draw in this way.

Example 1:

1
2
3
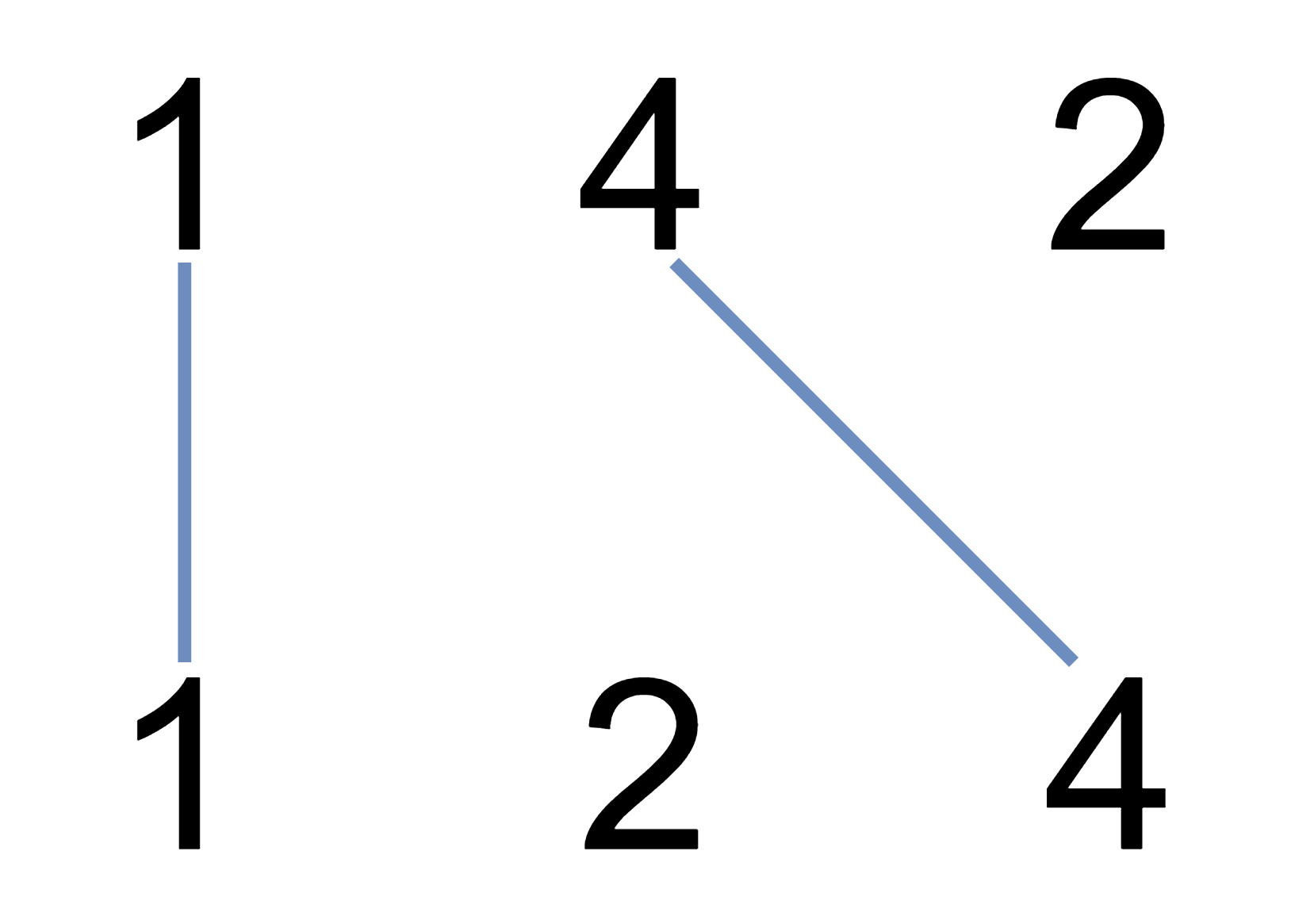
4
Input: A = [1,4,2], B = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from A[1]=4 to B[2]=4 will intersect the line from A[2]=2 to B[1]=2.

Example 2:

1
2
Input: A = [2,5,1,2,5], B = [10,5,2,1,5,2]
Output: 3

Example 3:

1
2
Input: A = [1,3,7,1,7,5], B = [1,9,2,5,1]
Output: 2

Note:

  1. 1 <= A.length <= 500
  2. 1 <= B.length <= 500
  3. 1 <= A[i], B[i] <= 2000

虽然题目看起来有点复杂，其实就是求最长公共子串的长度。连线互不交叉其实就是公共子串换了一种说法而已。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int maxUncrossedLines(vector<int>& A, vector<int>& B) {
        int row = A.size(), col = B.size();
        vector<vector<int>> dp(row + 1, vector<int>(col + 1, 0));
        for (int i = 1; i <= row; i++) {
            for (int j = 1; j <= col; j++) {
                if (A[i - 1] == B[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                else {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[row][col];
    }
};