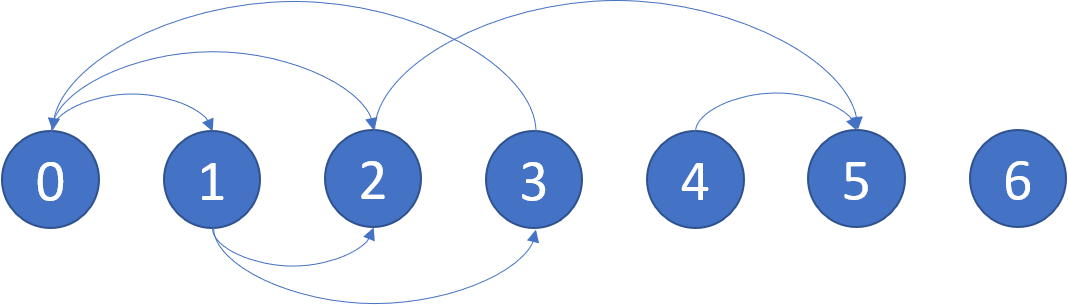
LeetCode 802. Find Eventual Safe States

In a directed graph, we start at some node and every turn, walk along a directed edge of the graph. If we reach a node that is terminal (that is, it has no outgoing directed edges), we stop.

Now, say our starting node is *eventually safe *if and only if we must eventually walk to a terminal node. More specifically, there exists a natural number K so that for any choice of where to walk, we must have stopped at a terminal node in less than K steps.

Which nodes are eventually safe? Return them as an array in sorted order.

The directed graph has N nodes with labels 0, 1, ..., N-1, where N is the length of graph. The graph is given in the following form: graph[i] is a list of labels j such that (i, j) is a directed edge of the graph.

Example:
Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]]
Output: [2,4,5,6]
Here is a diagram of the above graph.

Note:

• graph will have length at most 10000.
• The number of edges in the graph will not exceed 32000.
• Each graph[i] will be a sorted list of different integers, chosen within the range [0, graph.length - 1].

这道题可以用找环来解决，所有在环中的node和后继node有在环中的node都不是safe的。使用DFS来搜索环，遇到已经判断过的就不需要再继续搜索。

class Solution {
    vector<int> circle;
    vector<int> visited;
public:
    vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
        circle.assign(graph.size(), 0);
        visited.assign(graph.size(), 0);
        unordered_set<int> path;
        for (int i = 0; i < graph.size(); i++) {
            dfs(graph, path, i);
        }
        vector<int> ans;
        for (int i = 0; i < circle.size(); i++) {
            if (!circle[i])
                ans.push_back(i);
        }
        return ans;
    }

    void dfs (vector<vector<int>>& graph, unordered_set<int> &path, int node) {
        if (visited[node]) {
            if (circle[node] || path.count(node)) {
                for (auto i : path) {
                    circle[i] = 1;
                }
            }
            return;
        }

        visited[node] = 1;
        path.insert(node);
        for (auto i : graph[node]) {
            dfs(graph, path, i);
        }
        path.erase(node);
    }

};